smth1, smth3, smthn functions
smth1(input, averaging [, initial])
smth3(input, averaging [, initial])
smthn(input, averaging, n [, initial])
Arguments:
input: the value to be smoothed
averaging: time over which to smooth the input value
n (smthn only): order of the material smoothing
initial (optional): the value of the result when the function first applies
Result:
The smoothed value of input.
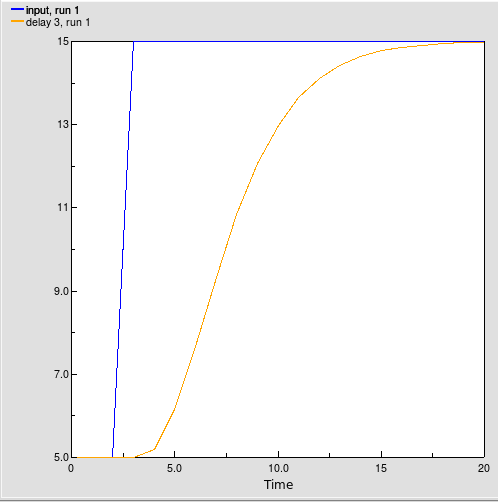
The smth1, smth3 and smthn functions perform a first-, third- and nth-order respectively exponential smooth of input, using an exponential averaging time of averaging, and an optional initial value initial for the smooth. smth3 does this by setting up a cascade of three first-order exponential smooths, each with an averaging time of averaging/3. The other functions behave analogously. They return the value of the final smooth in the cascade. If you do not specify an initial value initial, they assume the value to be the initial value of input.
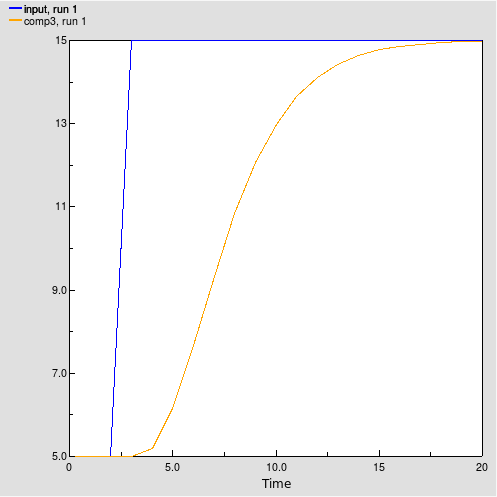
The smth3 function will return the value of comp3 in the structure and equations shown below.

Compartment comp1 :
Initial value = initial (real)
Compartment comp2 :
Initial value = initial (real)
Compartment comp3 :
Initial value = initial (real)
Flow flow1 :
flow1 = (input-comp1)*3/averaging (1/day)
Flow flow2 :
flow2 = (comp1-comp2)*3/averaging (1/day)
Flow flow3 :
flow3 = (comp2-comp3)*3/averaging (1/day)
Examples:
Smooth_of_Step = smth3(Step_Input,5)
where
Step_Input = 5 + step(10,3) produces the pattern shown below.