In this model, the population is represented by a single compartment, representing the total number of animals in the population or the population density (number per unit area). Reproduction is assumed to be density dependent (the reproductive rate per individual, r, declines as population size increases), whereas mortality is not (the mortality rate per individual, m, is independent of population size).

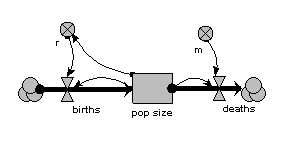
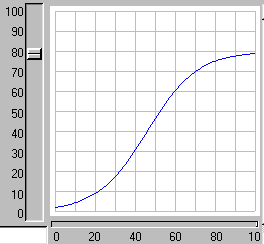
When the model is run, it shows the expected logistic form of population growth. When there are 80 individuals in the population, the birth rate balances the death rate.

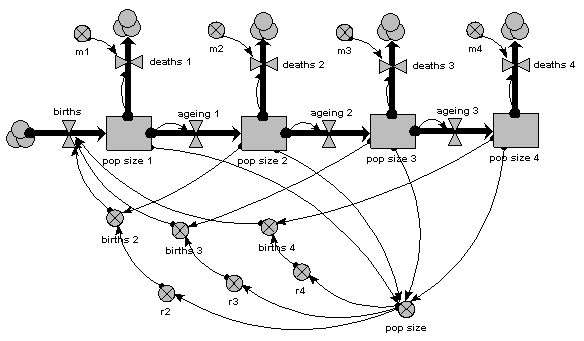
The same population is now represented by four compartments, one for each of four age classes. The first one represents the first year group, the second represents the number of animals aged 1-5 inclusive, the next animals aged 6-15 inclusive, and the fourth for all remaining animals. As before, the mortality rate per animal is independent of population size, but now depends on its age (there is a different m value for each age class). The reproductive rate per individual is still influenced by total population size, as well as now being different for each age class. Note that the first age class does not reproduce, so we simply do not include its reproductive rate.

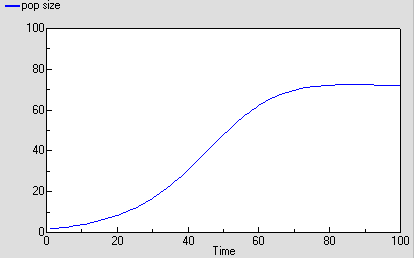
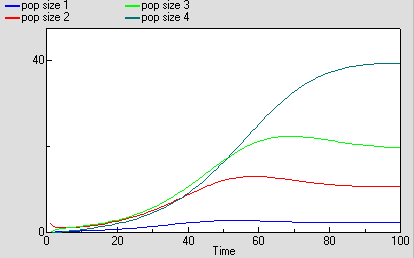
As before, we can now run the model and plot the dynamics of the total population size: this is in the variable called “pop size”, which is simply the sum of the population sizes for each age class. This again shows logistic growth: it will differ in detail, since the single-valued parameters we had before are now different for each age class.

But we are now able to inspect the dynamics for each of the four age classes. We see that the stable total population size is reflected in stable numbers in each of the four age classes, with different numbers in each class reflecting their different population parameters. Notice that there is some overshoot before the stable values are reached.

The above two examples are expressed in conventional System Dynamics terms. They set the scene for the next three, which are now expressed in terms unique to Simile.

The second example had just four age-classes, but already we can start to see some problems. First, the diagram is starting to get a bit messy: this would get worse if, for example, the mortality rates were also density-dependent. Second, any change to one of the basic equations, such as that for working out the birth rate per individual, has to be done separately for each age class. We can easily see that this approach does not really scale up to a larger number of classes: for example, if we decided to have one-year classes for the whole population. What we would like to have is a way of specifying once how an age-class works, then get this repeated automatically across all age classes.

In other visual modelling environments, this is done by allowing the user to specify that some variables are in fact arrays. In Simile, the approach is to specify the compartment-flow structure in a submodel for one age-class in terms of scalar (single-valued) variables, then specify that the submodel has multiple instances, one for each age class.

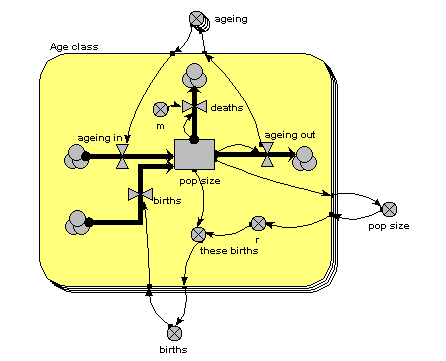
The main thing to note about this diagram is that it now has just one compartment. This is in a multiple-instance submodel, called “Age class”, with four instances, one for each class. The variable “pop size” inside the age class submodel represents the population of each age class; the variable with the name “pop size” outside the submodel represents the total population size (and is the sum of the population sizes for each age class).

What previously was a single ageing flow connecting two successive compartments is now two flows: one for the number leaving a compartment through ageing (“ageing out”), the other for the number entering a compartment from the class below (“ageing in”).

How does the “ageing in” flow for one age class know what the “ageing out” flow is for the class below it? This is clearly central to the whole model: everything else can be done on a class-by-class basis, but this involves some form of connection between classes. And we can't do that inside the submodel, since each instance can only know about its own values, not those of other instances. The answer is to take the “ageing out” values outside the submodel, and put them into an array (“ageing”). This array is them made available to the “ageing in” flow, which extracts the value for the previous class.

There is a births inflow for each age class. This is required since we are modelling a generic age class, but in fact the equation for this flow sets it to zero for all classes except the first. This flow is derived from the total births, which is held in the variable outside the age class submodel: that in turn is calculated from the sum of “these births”, which is the number of births for each of the age classes. Remember in the previous model how the first age class did not reproduce, so we simply left off the variables for it? We can’t do that now: instead, we set the parameter value r to zero for the first class.

The behaviour of this model is identical to the previous version, in which we had a separate compartment for each age class. We have not changed it mathematically: merely the way it has been implemented.

The previous method is a big improvement: it is a much more concise way of representing multiple age classes, and exactly the same model can be used regardless of the number of classes we have: in other words, it scales up to larger problems. However, it suffers from a couple of disadvantages:

1. There is a problem with the amount of data flowing around. Let’s say that we have 100 classes. Then Simile has to handle 100x100 values, since it has to make the array holding the 100 values available to each of the 100 classes. This is actually manageable, but still involves a lot of unnecessary computation (when we consider that in fact that there are only 100-1 = 99 interactions between classes, one for each pair of ageing transitions).
2. Our model diagram does not really convey the fact that there is a special relationship between classes, namely that one class is immediately above the previous one. Class 2 is above class1, class 3 is above class 2, and so on. There is no connection between class 1 and class 3. Since this is an important feature of our model, and since one aim of the model diagram is to convey information about the model design down to a certain level, it would be nice if the model diagram showed that some form of relationship existed between classes.

Simile’s association submodel provides a way for tackling both problems. This is quite a big step in your understanding of Simile if you have not come across it before, particularly if you have no background in relational databases or the concept of “association” in object-oriented software engineering. So all I will do here is to present the model diagram and talk you through that: an explanation of the equations used can wait until you actually come to use it.

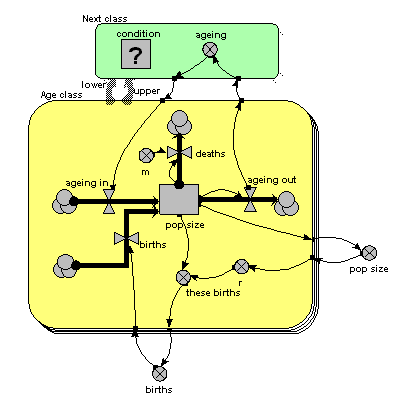
The only difference from the previous model is that the single array variable, holding all the ageing flows from one age class to the next, has been replaced by am ageing variable inside another little submodel, called “Next class”. This is made with Simile’s submodel tool, just like any other submodel. It is, however, different in two respects from other submodels. First, it has two broad grey arrows pointing to it from the “Age class” submodel. These indicate that there is an “next class” relationship (or “association”) between one class (the lower one) and another (the upper one). Second, we see that the submodel contains a condition element: this is used to specify the condition under which the “next class” relationship holds true. In fact, it holds true if, and only if, the instance number of one class is just one higher than that of another class: that condition is entered in the Equation box for the questionmark symbol.

What happens is that all the values for “ageing out” are passed to the submodel, but only one value is passed back into the submodel for each class: the one for the class above it.

You will have noticed that the model diagram does not itself tell us just what relationship exists between classes. However, it does tell us that some sort of relationship exists between them, so the diagram has helped in communicating the nature of the model down to a certain level. This is rather like when we have a variable with influences on it: we can see that the influences exist, without seeing the actual equation used to capture their effect.

The above examples all share one thing in common: they represent a population in terms of the values for one or more state variables, there being as many state variables as there are classes in the population. Each state variable may be engineered to have integer values (on the basis that populations contain a discrete number of individuals), or to have real (floating point) values, if you are content to think in terms of population density (i.e. number per unit area) rather than absolute numbers. The number of state variables (hence the computational requirement) is fixed, and totally independent of the number of individuals in the population.

A totally different approach is to represent each individual in the population separately. This can be justified on the basis of what is considered necessary to adequately capture the factors driving population dynamics. For example, if we know that social interactions between individuals is important, then we need some way of capturing these: it may be difficult to approximate to their effects in a lumped or class-disaggregated model.

Since we are interested in population dynamics, building an individual-base model will require that we create new individuals as time goes on, and remove existing ones. Thus, the amount of memory required to manage this population will change as the simulation proceeds. If the model is implemented by programming, the difficulty of doing this increases substantially as we move from a fixed number of state variables to a dynamically-changing list.

In Simile, it is very easy to create an individual-based model. You simply use a Simile submodel to define how one individual works, then declare this submodel to be a population submodel. You can then add model elements to hold the equations or rules for the creation of new individuals and the killing off of existing ones.

Here’s a model which is the individual-based equivalent of the age-class model with density-dependent reproduction. We make a submodel and call it “Individual” (following the principle that the label for a multiple-instance submodel should reflect the single object it references). It is specified as a population submodel by simply choosing this option in the submodel properties box. A population submodel is drawn with shadow lines on the top-left and bottom-right, to distinguish it from the fixed-membership multiple instance submodel we have seen so far.

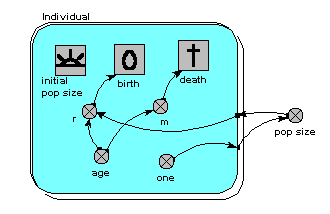
It has symbols for representing the initial number (i.e the number created when the model is initialised), an expression for creating new individuals by reproduction of existing ones (“birth”), and an expression for deciding when an individual dies (“death”). For consistency with the notation of the earlier models, we have two parameters, r and m, with similar meaning as before: r represents the probability that an individual will reproduce in one unit of time, and m represents the probability that an individual will die. Both r and m depend on the individual’s age (calculated simply as the difference between the current simulation time and the time when the individual was created). r also depends on the size of the population (negative density dependence). The population size is calculated as the sum of the value 1 (held in the variable “one”) over all the individuals. Note that population size has to be outside the individual submodel, since it is an attribute of the whole population, not of any one individual.

This model is now a stochastic one: the parameters r and m are treated as probabilities rather than deterministically generating changes to the population. We could have handled these deterministically - for example, creating one new individual when we had accumulated sufficient credit — but a stochastic interpretation is more intuitive. We could also have made the previous models stochastic (by sampling from a distribution to get the annual reproductive inputs and mortality losses), but then we would have lost the link with standard textbook models of population dynamics.

You may be surprised to see that there are no compartments here. We could have them: for example, we may want to model the change in body weight of each individual (or, say, height of each tree), in which case we could have a compartment and associated flows inside the submodel. We could equally well choose to have a complex System Dynamics model if, for example, we have a sophisticated, physiologically-based model of tree growth and we want to model a stand of trees on that basis. But this example shows that we do not have to include compartments and flows in a Simile model. Nevertheless, we can still use part of System Dynamics notation: the variable and the influence arrow.

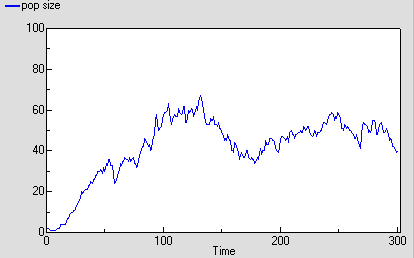
The following graph shows one run with the model. It’s run for 300 time units, since the reaching of an asymptote after 100 time units is less clearcut with this stochastic model. Even then, its stochastic nature means that there is considerable variation after reaching balance.

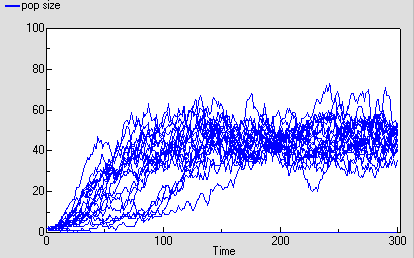
The following diagram shows the result for 25 replicate runs. The basic logistic growth can be discerned. It is also clear that the stochastic nature is more than simply variation around this line: some runs take quite a while to take off, and in fact in some cases the population goes extinct.

These five examples have demonstrated a number of important points.

1. First, the population modeller can construct very different models based on more-or-less the same biological assumptions. The above models all have negative density-dependence for reproduction and density-independent mortality, but differ in their degree of disaggregation and the age-dependency of population processes. The modeller should be aware of these choices, and ideally be able to justify a choice vis-a-vis the alternatives.
2. Second, mathematically-identical models (the three age-class models) can be implemented in different ways. These do not affect the results produced, but do affect the ease of working with the model and the ease of communicating the model to others. Again, the modeller should be aware of such choices.
3. Third, Simile is unusual — if not unique — in enabling these very different models to be constructed within a single, easy-to-use environment. This minimises the amount of effort the modellers have to put in to explore these alternative approaches, compared with having to use different packages, or implementing the different models in a programming language.

Finally, we can broaden our vision beyond the modelling of one population. Usually, a population model will be a component of some larger system: the food on which the population depends; other predator populations; various abiotic factors; possibly even human factors (for example, in farming systems or wildlife conservation). Any of the population models we have considered above could be integrated into a larger, ecosystem model. Moreover, it could be wrapped up in an outer submodel envelope, and the alternative versions could be swapped in and out of the ecosystem model on a plug-and-play basis: another strong argument for enabling different modelling approaches to be implemented within a single modelling environment.