3. Age classes, with a multiple-instance submodel
The above two examples are expressed in conventional System Dynamics terms. They set the scene for the next three, which are now expressed in terms unique to Simile.
The second example had just four age-classes, but already we can start to see some problems. First, the diagram is starting to get a bit messy: this would get worse if, for example, the mortality rates were also density-dependent. Second, any change to one of the basic equations, such as that for working out the birth rate per individual, has to be done separately for each age class. We can easily see that this approach does not really scale up to a larger number of classes: for example, if we decided to have one-year classes for the whole population. What we would like to have is a way of specifying once how an age-class works, then get this repeated automatically across all age classes.
In other visual modelling environments, this is done by allowing the user to specify that some variables are in fact arrays. In Simile, the approach is to specify the compartment-flow structure in a submodel for one age-class in terms of scalar (single-valued) variables, then specify that the submodel has multiple instances, one for each age class.
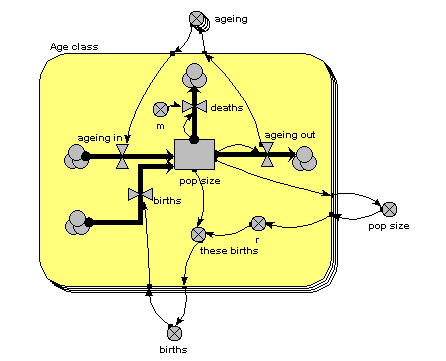
The main thing to note about this diagram is that it now has just one compartment. This is in a multiple-instance submodel, called “Age class”, with four instances, one for each class. The variable “pop size” inside the age class submodel represents the population of each age class; the variable with the name “pop size” outside the submodel represents the total population size (and is the sum of the population sizes for each age class).
What previously was a single ageing flow connecting two successive compartments is now two flows: one for the number leaving a compartment through ageing (“ageing out”), the other for the number entering a compartment from the class below (“ageing in”).
How does the “ageing in” flow for one age class know what the “ageing out” flow is for the class below it? This is clearly central to the whole model: everything else can be done on a class-by-class basis, but this involves some form of connection between classes. And we can't do that inside the submodel, since each instance can only know about its own values, not those of other instances. The answer is to take the “ageing out” values outside the submodel, and put them into an array (“ageing”). This array is them made available to the “ageing in” flow, which extracts the value for the previous class.
There is a births inflow for each age class. This is required since we are modelling a generic age class, but in fact the equation for this flow sets it to zero for all classes except the first. This flow is derived from the total births, which is held in the variable outside the age class submodel: that in turn is calculated from the sum of “these births”, which is the number of births for each of the age classes. Remember in the previous model how the first age class did not reproduce, so we simply left off the variables for it? We can’t do that now: instead, we set the parameter value r to zero for the first class.
The behaviour of this model is identical to the previous version, in which we had a separate compartment for each age class. We have not changed it mathematically: merely the way it has been implemented.