Lorenz strange attractors
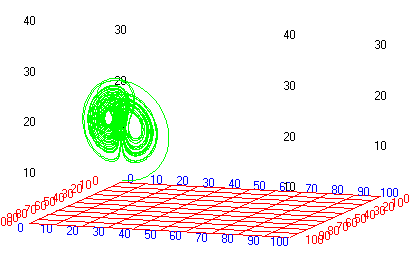
In 1963 the meteorologist and mathematician E. N. Lorenz published solutions for a simplified mathematical model of atmospheric turbulence in an air cell under a thunderhead. The model is now generally known as an illustration for chaotic behaviour and strange attractors.
The basic equations are:
|
d(x1)/dt = a*(x2-x1) |
|
d(x2)/dt = (r-x3)*x1-x2 |
|
d(x3)/dt = x1*x2-b*x3 |
where:
- x1 is the amplitude of the convective air currents
- x2 is the temperature difference between the rising and falling currents
- x3 is the deviation of temperature from the mean
- a, r and b are dimensionless physical parameters
For more information, see http://mathworld.wolfram.com/LorenzAttractor.html.
Download the model file and explore the behaviour of the strange attractor using Simile’s included XY-plotter, as set-up by this display configuration file.
| Files : | lorenz.zip |