Graphical Modelling in Simile : Discrete event based
Event-based modelling in Simile
A pure discrete-event-based model includes only event symbols (time series and derived/delayed) and states. An event symbol only has a value at the point in time at which it occurs. The value of a derived event occurrence is calculated by its equation, which can include the value of the triggering event occurrence. A state has a rule for each event symbol that influences it. When an influencing event occurs, the state's new value is given by the corresponding rule, otherwise it stays the same.
A model that mixes system dynamics (continuous) and discrete-event based operation also includes limit event symbols and squirts. A limit event occurrence is triggered when its equation reaches its minimum or maximum value, allowing continuous processes to set off events. A squirt is a derived event which causes an instantaneous transfer of material between compartments, allowing events to affect continuous processes. State changes can also affect continuous processes, but only squirts can cause discontinuities in the values of compartments.
See also the 5th video in the Simile Tutorial Series.
|
|
An instantaneous occurrence which can have a magnitude |
|
|
|
A quantity set by events according to rules |
|
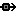 |
squirt | An instantaneous transfer of a substance between compartments |
 |
If an influence originates from a discrete event valued component, it is shown 'bulged' to indicate that it carries a discrete event value. Such an influence cannot terminate on a continuous-valued component. | |
|
|
The channel components which specify changes to the membership of population submodels can be either continuous or discrete valued. If one or more discrete valued influence terminates on one of these, it is discrete valued and behaves like a squirt component, adding or removing as many submodel members immediately as the continuous version would over one time unit. |
|
|
|
||
|
|
||
In: Contents >> Graphical Modelling
Discrete event-based modelling : Event element
 Event
Event
How to add an Event symbol
See Adding node-type elements.
Interpretation
An event symbol represents something that happens at an instant in time, such as the arrival of a package. The event represented by a symbol may occur any number of times during a model run, or not at all. An event occurrence can have a numerical magnitude, and having a magnitude of zero is the same as not occurring. The effects of an event occurrence can be proportional to its magnitude. Alternatively it can be boolean, i.e., all-or-nothing. Event symbols should not have array equations, but can go in multi-instance submodels, in which case the event can occur independently in each instance of the submodel.
In system-dynamics models, time advances by regular steps. When an event is about to occur, Simile will execute a time step with a size that will advance the time to exactly the point at which the event is predicted to occur, in order that the effects of changes made by the event are not subject to time step rounding errors.
There are three types of event, which differ in how they are triggered. The equation dialogue for an event includes radio buttons to select between these event types, and they are distinguished by different 'decorations' on the event symbol in the model diagram.
|
Modelling use |
Set-up of "event" |
|
The exact time at which the event occurs is determined by extrapolation of the equation value over the previous system-dynamics time step. If the integration method is Euler, linear extrapolation is used; if Runge-Kutta, it is done by a quadratic approximation. If adaptive step-size variation is selected, a check is done that the crossing actually occurs around the predicted time, and the time step is re-calculated with a new prediction if the difference is too great. |
Only has inflluence arrows from continuous valued components One or more influence arrows pointing from it to other events, squirts or states Magnitude is on/off if one limit supplied, integer of -1 or 1 if both limits supplied |
|
If a time series event symbol is put inside a multi-instance submodel, the values in the series must be arrays with the dimensions of the submodel. At each time point in the series, the event will occur in all instances of the submodel for which the corresponding array element is non-zero (or 'true' if type is boolean). |
No influence arrows pointing to it. One or more influence arrows pointing from it to other events, squirts or states. Occurrence times and magnitudes given by series data |
 Derived event (No decorations): This is an event that occurs as a result of other event occurrences. It must have an influence from at least one other event or squirt, and may occur whenever any of them occur. It may also have influences from other components, whose values may be used in its equation. Its equation is evaluated when it is triggered, and gives its magnitude. The equation cannot refer to event values directly, but can include the special function 'trigger_magnitude()' which gives the magnitude of the triggering event, or their sum if more than one happens simultaneously. If the trigger magnitudes sum to zero, or the equation evaluates to zero (or 'false' if type is boolean) the event will not occur. Derived event (No decorations): This is an event that occurs as a result of other event occurrences. It must have an influence from at least one other event or squirt, and may occur whenever any of them occur. It may also have influences from other components, whose values may be used in its equation. Its equation is evaluated when it is triggered, and gives its magnitude. The equation cannot refer to event values directly, but can include the special function 'trigger_magnitude()' which gives the magnitude of the triggering event, or their sum if more than one happens simultaneously. If the trigger magnitudes sum to zero, or the equation evaluates to zero (or 'false' if type is boolean) the event will not occur.The equation of a derived event can be of the form after(t,x) where t and x are subexpressions. In this case the magnitude of the event is x at the time of triggering, but it does not occur until t time units later. This is the only context in which after(...) can be used. |
Must have an influence from at least one other event or squirt, can have other influences to it One or more influence arrows pointing from it to other events, squirts or states. |
In: Contents >> Graphical Modelling >> Discrete-event based
Discrete event-based modelling : Squirt arrow
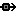 Squirt arrow
Squirt arrow
How to add a Squirt arrow
See Adding arrow-type elements.
Interpretation
The squirt arrow is used to specify where event occurrences cause sudden changes to the value of a compartment. If the squirt arrow enters a compartment, it specifies a positive step change to that compartment. If it leaves the compartment, it specifies a negative step change (unless the magnitude of the squirt occurrence is negative in which case these directions are reversed, as for a negative flow value). Many aspects of using squirts are similar to using flows.
If your model needs to keep track of changes in the amount of a substance but you are not interested in where it comes from or goes to, your squirt arrow may start or finish on a blank part of the model diagram. In this case a "cloud" will be drawn at the end point, indicating that the amount of substance there plays no role in the model. Each cloud may only have one flow or squirt connected to it.
Influences to and from a squirt arrow are attached to a "target" (or "bulb") symbol which is positioned on the squirt arrow. This represents the point that generates the transfer. Influences from a squirt arrow start from this point and are used in the same way as those from an event symbol, and must go to other squirts, events or states.
In most respects, a squirt is treated just like a derived event. You can use the full range of the equation language when you enter an equation for the squirt, including the trigger_magnitude() and after() functions, just as you can do for a derived event. The two differences are that:
- a squirt is the only way you can express an instantaneous change term for a compartment; and
- a squirt cannot be a time series event or a limit event.
Rules
- A squirt arrow can only be drawn into and/or out of a compartment.
- Influences can be drawn to a squirt's bulb, and must include one from another squirt or event symbol.
- Influences can be drawn from a squirt's bulb to other squirts, events or states.
- The units for a squirt value must be of the same dimensions as the units of the corresponding compartment(s) that it is linked to. For example, if you have a squirt going into a compartment whose units are kg, and the unit of time for the model is a year, then the units for the squirt can be kg, g, lb etc. An automatic conversion will be performed if necessary. The time units do not matter (unlike flow units) because the transfer is instantaneous.
In: Contents >> Graphical Modelling >> Discrete-event based
Discrete event-based modelling : State element
 State
State
How to add a State symbol
See Adding node-type elements.
Interpretation
A state is a model value that is changed by events, but otherwise stays the same. A state does not have a unique equation, but rather a set of rules, each consisting of an event (the trigger) matched with an equation (the effect). There will be one rule for each event that influences the state, plus an extra effect labelled "reset..." that sets the initial value of the state when the model resets (or when a new instance of the state's parent submodel is created).
In the equation dialogue for a state, the influencing event symbol captions (and reset...) are listed to the left of the equation field, and clicking on an event caption shows the effect for an occurrence of that event. In the equation bar, a pull-down menu to the left selects the caption of the event whose effect is to be edited. The popup text for the state is a condensed form of the rules, e.g., "9 on event1, 6 on event2, 0 on reset."
Components with continuous values can also influence the state, and their values can be used in one or more of its effect equations.
The value of a state after an event occurrence depends only on the effect equation of that event, and not on its previous value. However the equation can use the prev(0) function to refer to the state's previous value if the new value is to be a function of it. The equation can also use the trigger_magnitude() function to refer to the magnitude of the triggering event occurrence if this is to affect the state's new value. The effect equations cannot use the after(t,x) function; the state's value always changes immediately after the triggering event occurs.
Currently the order in which the rules are applied if multiple triggerring events occur simultaneously is undefined.
Rules
- A state must have influences from at least one event or squirt symbol
- A state must have an equation for each event or squirt symbol influencing it, plus one for reset
- Other components (including other states) can influence it, and their values can be used in its equations
- All of its equations must evaluate to quantities with the same units and dimensions
- A state can influence any other component
In: Contents >> Graphical Modelling >> Discrete-event based
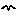


 Limit event : This represents an event that occurs when a model value reaches some pre-set limit. It requires an equation and a minimum and/or maximum value to be entered. The event occurs when the value of the equation reaches the minimum or maximum, and the event should cause the value to go no further in that direction. The event is boolean (i.e., has no magnitude) if only one limit is present. If both are present its magnitude is -1 at the lower limit and 1 at the upper limit. Hence its equation does not affect its magnitude, only its time of occurrence.
Limit event : This represents an event that occurs when a model value reaches some pre-set limit. It requires an equation and a minimum and/or maximum value to be entered. The event occurs when the value of the equation reaches the minimum or maximum, and the event should cause the value to go no further in that direction. The event is boolean (i.e., has no magnitude) if only one limit is present. If both are present its magnitude is -1 at the lower limit and 1 at the upper limit. Hence its equation does not affect its magnitude, only its time of occurrence. Time series: This gets its values from outside the model like a
Time series: This gets its values from outside the model like a  'zap' button.
'zap' button.