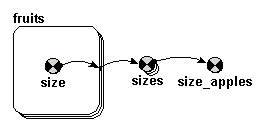
element function
element([X],I)
Picks the Ith value from the array [X]
Inputs: an array [X] of any type
integer I
Result: type
Examples:
element([10,20,30,40],3) --> 30 (since 30 is the value of the 3rd element of the array.
element([[1,2], [3,4], [5,6]],2) --> [3,4] (since the array [3,4] is the 2nd element of the input array)
element([10,20,30,40],index(1)) --> 10 for the first instance of a four-instance submodel, 20 for the second instance, etc, since index(1) has the value 1 for the first instance, 2 for the second instance, etc.
Comments:
This is an essential function for use with multiple-instance submodels, in which case it is almost always used in combination with the function index(1) in the second argument. One common use is to provide each instance of a multiple-instance submodel with a unique value for some parameter or other value. The third example (above) illustrates this: that could, for example, be the expression in a compartment element inside a four-instance submodel, initialising the compartment for each of the four instances to 10, 20, 30 and 40 respectively.
For advanced users:
The element function has rather more power than suggested above. The second argument can act as a sort of template to say how values (or sub-arrays) from the first argument are to be picked up. This is illustrated by the following example:
element([3,2,7,4,9,34,1,5], [[5,2], [1,5]]) --> [[9,2], [3,9]]
If the first argument is multidimensional and the second argument is a one-dimensional array, the elements of the second argument will be used to pick elements from the innermost arrays of the first argument from whuch to build the result, e.g.,
element([[3,5,11], [1,2,8]], [2,1,2]) --> [1,5,8].
The reason it works this way is that the converse behaviour, i.e., each element of the second argument selecting a value from the corresponding element of the first argument, is easy to get in the case where the first argument is a value from a nested submodel by putting the element() function inside the outer submodel, and can be obtained in general by building up from simple cases, e.g.,
makearray(element(element([[3,5,11], [1,2,8]],place_in(1)), element([3,1], place_in(1))), 2) --> [11,1].
makearray(element([[5,7],[1,4],[8,5]], element([3,3,2,2], place_in(1))), 4) --> [[8,5], [8,5], [1,4], [1,4]]
Use of element() on lists
Starting with Simile version 6.1, it is possible to have a list-valued expression as the first argument of element(), in which case the result is a sublist of that list, i.e., a list containing some, all or none of the members of the original list in the same order. The second argument can be a single value, in which case the resulting list has one element if the list includes a value with that index, and none otherwise. So applying sum() to it gives either a value from the original list or zero.
If the second argument is an array or list, the result is a sublist of the first argument containing all the values whose indices appear as values in the second argument. There are a few points to note about all these uses:
- It is not computationally efficient. The values from the list are found by searching through it sequentially rather than by lookup as can be done on arrays.
- If the second argument is an array or list, its values must be in ascending order, or in the order in which they appear in the definition if they are of an enumerated type. If a value occurs more than once in the second argument, the value with that index will still only appear once in the result. This is because rather than searching the list from the start for each value, the generated code merely starts from where the last one was found, since the indices in the original list should always be in ascending order. (This does not apply when selecting a sublist from a list of neighbour values in a special-purpose submodel; the direction identifiers can be in any order, and if one occurs more than once, its value from the original list will also be repeated).
- The resulting list cannot itself be used as the first argument of element(), or arithmetically combined with other list-valued expressions.
element() with multiple indices
Starting with Simile version 6.1, if you have a 2-D (or higher) array, you can look up a single member by using element() with 3 (or more) arguments, e.g.,
element([[arr]], x, y)
Formerly you would have had to do this by nesting element() calls, but the new format is neater and allows the indices to be matching arrays or lists themselves to get multiple values.
Examples:
element([[6,1,8],[7,5,3],[2,9,4]], 2, 2) --> 5
element([[6,1,8],[7,5,3],[2,9,4]], [2,1,3], [3,1,2]) --> [3,6,9]
In: Contents >> Working with equations >> Functions >> Built-in functions

 button, or hit return, to set the equation.
button, or hit return, to set the equation. button if you make a mistake. It restores the previous entry.
button if you make a mistake. It restores the previous entry. button.
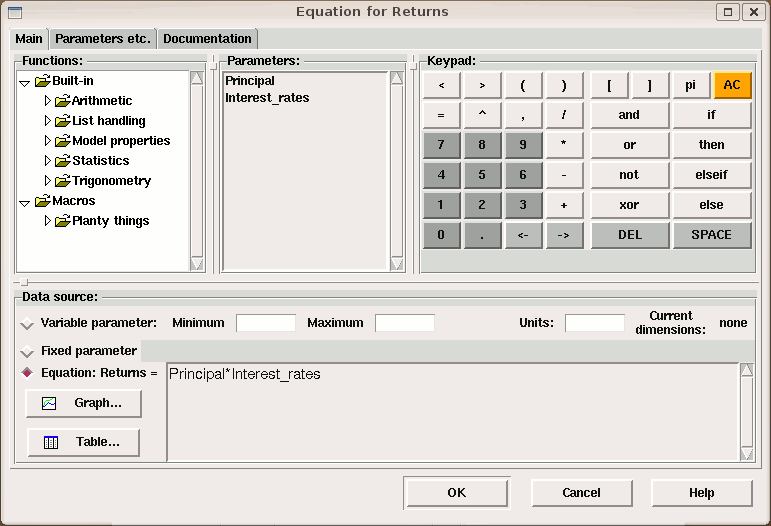
button.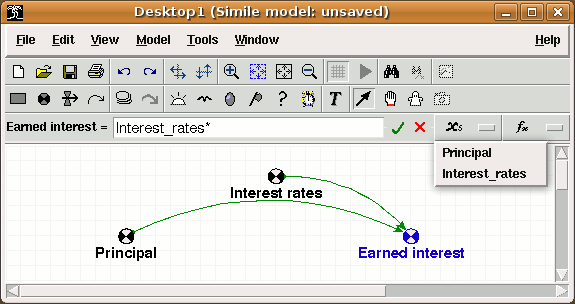
 button. The top level of this cascade also contains an entry labelled "Enum. type constants", for adding the names and members of any
button. The top level of this cascade also contains an entry labelled "Enum. type constants", for adding the names and members of any 





 pull-down menu button on the
pull-down menu button on the 
 Array-valued components
Array-valued components