Built-in functions : hypot function

hypot function

hypot(X,Y)

Returns length of hypotenuse of right-angle triangle with base X and height Y

Inputs: numeric, numeric

Result: numeric

Examples:

hypot(3,4) --> 5 (a 3:4:5 triangle)

hypot(x1-x2,y1-y2) --> the distance between two points with co-ordinates (x1,y1) and (x2,y2) respectively.

hypot(x-[xs],y-[ys]) --> [distances] I.e. an array containing the distance from one point with co-ordinates (x,y) to a set of points, with co-ordinates held in the arrays [xs] and [ys]. See comments.

Spatial modelling frequently requires that one object knows the distance to another. This requires that each has x,y co-ordinates. It is then simple to use the hypot function to work out the straight-line distance between them, as shown in the second example above.

The same principle applies when you use a multiple-instance submodel to represent a set of spatially-located objects. In this case, each object may want to know how far it is to all the other objects - for example, in working out the competition between trees in an individual-based tree model. The following model diagram fragment shows a typical model configuration for doing this:

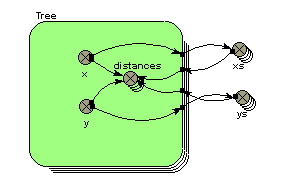
Each tree has x,y co-ordinates. These are exported to two array variables, xs and ys, whose equations are simply:

xs = [x]

and

ys = [ys]

These arrays are then brought back into the submodel, and used to generate an array containing the distance for each tree to all the other trees, using the equation given in the third example above.

In: Contents >> Working with equations >> Functions >> Built-in functions