Main menu
You are here
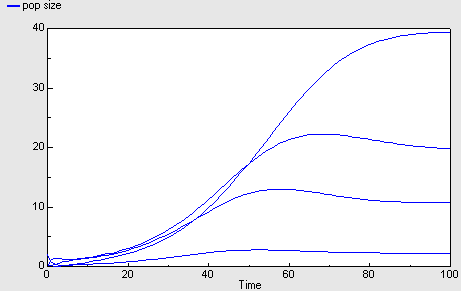
Age-class model of population dynamics, using a multiple-instance submodel and an association submodel
This models a population of animals in terms of four age-classes. For each age-class, we use a compartment (state variable) to represent the number of individuals in that class. This version uses a four-instance submodel to represent the four age-classes. The ageing flow (from one class to the next) thus has to be handled by transferring the value for the outflow from each class to be assigned to the inflow for the next class. In this model, this is done by using an association submodel to represent the fact that each age class is 'associated' with the next one (by virtue of the fact that the next class receives the animals that have aged out of the previous class). The value for the number of animals leaving progressing from one class to the next is then passed through this submodel.
Equations in Desktop
births = sum([these_births])
pop size = sum([pop_size])
Equations in Age class
pop size: initial value = element([2,0,0,0],index(1))
ageing in = sum({ageing_next})
Where: {ageing_next}=../Next class/ageing (to Age class in next)
ageing out = element([1,0.2,0.1,0],index(1))*pop_size
births = if index(1)==1 then births else 0
deaths = m*pop_size
class = index(1)
m = element([0.05,0.01,0.01,0.05],index(1))
r = element([0,0.05,0.2,0.1],index(1))*(1-total_pop_size/100)
these births = r*pop_size
Equations in Next class
condition = class_next==class_this+1
Where: class_this=../Age class/class (from Age class in this) class_next=../Age class/class (from Age class in next)
ageing = ageing_out_this
Where: ageing_out_this=../Age class/ageing out (from Age class in this)
here: ageing_out_this=../Age class/ageing out (from Age class in this)/
| Attachment | Size |
|---|---|
 ageclass6.sml | 64.16 KB |
| ageclass6.shf | 3.49 KB |