Main menu
You are here
Fire spread -- rectangular grid
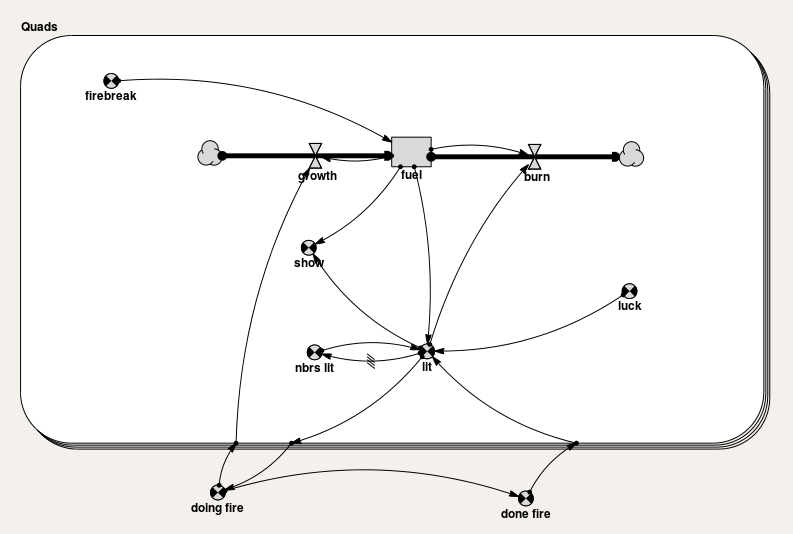
This is a very simple model of fire spread in a patch of vegetation. The model consists of a rectangular array of grid squares, created using the rectangular array built-in type. Vegetation in each square is modlled by a single compartment with a growth function that produces a sigmoid curve in the absence of any burning.
A square can catch fire either by a random event, or from its neighbouring squares. In each case the amount of fuel (vegetation) in the square is compared with a multiple of a fraction known as 'luck' and if there is more fuel, the square burns, resulting in a 50% reduction in vegetation. A square can burn multiple times during a single fire.
The model runs on a single time step, but the meaning of the time step changes during a fire, representing a much shorter interval. To implement this, the growth rate and the chance of a new spontaneous fire are set to zero while a fire is already burning.
A special variable, 'show', is used to display the vegetation. If a grid square is not on fire, this has the value of the vegetation compartment, which is between 0 and 100. If it is on fire, the value is -3. The grid display tool is set up with a colour scale from 0 to 100 representing vegetation states, then the scale is extended to -3 and the bottom-most swatch (covering only negative numbers since the scale is divided into 32 swatches) is set to orange to represent flame.
The model also includes a firebreak, an incomplete barrier down the middle of the grid. This is implemented by setting the initial vegetation for the squares within the barrier to zero. Because of the growth being a function of vegetation they keep this value and never burn. The incompleteness allows the model to illustrate that even an incomplete firebreak can act as a barrier most of the time.
Model Desktop1 :
Variable doing fire :
doing fire = any(any([[lit]])) (boolean)
Where:
[[lit]] = Value(s) of Quads/lit
Comments:
True if any square i the grid is on fire. Prevents normal growth or spontaneous ignition from happening (because timescale is shorter)
Variable done fire :
done fire = last(doing_fire) (boolean)
Where:
doing_fire = Value(s) of doing fire
Comments:
Take the last value of doing_fire here -- because using last(doing_fire) inside the submodel will cause an intermediate variable to be created for it in each instance, which wastes memory.
Submodel Quads :
Submodel "Quads" is a fixed_membership multi-instance submodel with dimensions [200,300].
Comments:
Each instance represents a square area of forest
Enumerated types: {rect_nbr sw s se w e nw n ne}
Compartment fuel :
Initial value = if firebreak then 0 else 4 (real)
Where:
firebreak = Value(s) of firebreak
Comments:
Because growth rate is a function of current load, setting the initial value in the firebreak area to zero ensures that it remains at zero.
Flow burn :
burn = if lit then 0.5*fuel/dt() else 0 (1/day)
Where:
fuel = Value(s) of fuel
lit = Value(s) of lit
Comments:
Half the fuel in a cell will be consumed if it catches; it might catch more than once in a single fire, causing uneven burn patterns.
Flow growth :
growth = if doing_fire then 0 else 0.001*fuel*(100-fuel) (1/day)
Where:
fuel = Value(s) of fuel
doing_fire = Value(s) of ../doing fire
Comments:
This function causes the fuel load to follow a sigmoid curve levelling out at 100 in the absence of fire. Fires happen much quicker than growth, so growth is set to zero while a fire is burning because model time takes on a different meaning.
Variable firebreak :
firebreak = column_id()>148 and column_id()<=152 and row_id()>4 (boolean)
Comments:
Incomplete firebreak down the middle of the simulated area.
Variable lit :
lit = not done_fire and luck*1e8<fuel or luck*200<fuel*last(nbrs_lit) (boolean)
Where:
nbrs_lit = Value(s) of nbrs lit
fuel = Value(s) of fuel
luck = Value(s) of luck
done_fire = Value(s) of ../done fire
Comments:
A cell will burn if its neighbours were burning last time step and it is unlucky, or if nothing was burning last time step and it is very unlucky (e.g., gets hit by lightning). More neighbours alight means more chance of burning. There must be more fuel available than luck!
Variable luck :
luck = rand_var(0,1) (real)
Comments:
Adds the random element; the lower it is, the more likely a cell is to burn.
Variable nbrs lit :
nbrs lit = howmanytrue({from_8_nbrs_lit}) (int)
Where:
{from_8_nbrs_lit} = Value(s) of lit
lit = Value(s) of lit
Comments:
Counts the number of a cell's eight neighbours which are alight.
Variable show :
show = if lit then -3 else fuel (real)
Where:
fuel = Value(s) of fuel
lit = Value(s) of lit
Comments:
For display purposes, The grid display should be set up with a range of -3 to 100 and the first swatch set to orange to represent fire. This variable will then show orange if the cel is burning, or a colour from a scale representing fuel load (black -> green -> straw) if not burning.
The fire on the left burnt when there was only just enough fuel to sustain it.
The one on the right is currently burning and covering a circular area because fuel is abundant.
| Attachment | Size |
|---|---|
| 104.72 KB | |
| 1.32 KB |
