Main menu
You are here
Lotka-Volterra two-species competition model
Thu, 23/08/2012 - 09:30 — jonathanm
ModelId:
competition1
SimileVersion:
3.1+
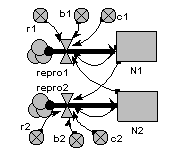
This is the classic textbook model of the population dynamics of two competing species.
It is based on a pair of differential equations, each having the same mathematical form:
dX1/dt = r1.X1.(1-b1.X1-c1.X2)
dX2/dt = r2.X2.(1-b2.X2-c2.X1)
where:
X1,X2 are the populations sizes of the two species;
r1,r2 are the intrinsic rate sof increase of the two species;
b1,b2 are the self-inhibition coefficients for the two species;
c1,c2 are the competitor’s inhibition coefficient for each species.
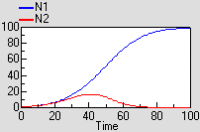
Results:
Weblinks:
Lotka-Volterra model of competitionSally Otto, Zoology, UBC, Canada. Rather more mathematically-based analysis of the model.
| Attachment | Size |
|---|---|
| 129.54 KB | |
| 2.01 KB |
