Main menu
You are here
Queueing for a group of ATM machines
This model illustrates the use of Simile to create pure event-driven models. There are no compartments or explicit references to time in the model, so the state only changes when an event occurs. This means that the setting of the "Update every:" period has no effect on the model behaviour.
The model represents a group of machines which people are arriving at random intervals to use. These could be ATMs outside a bank, automated checkouts at a supermarket, and so forth. The machines themselves are represented by instances of a submodel, so the model can be set to simulate any number of machines easily.
The three event nodes to the left of the model represent the arrival of customers. Since we want to simulate a situation in which they arrive at random, we want the intervals between arrivals to follow an exponential-random distribution. Simile can trigger an event after a certain delay following another event, using the after() function, so this is used to make each customer arrive the correct random interval after the last. The 'start' event is a limit condition that is always true, so it fires at the start of the simulation, triggering the delay to the arrival of the first customer.
When a customer arrives, one of two things can happen. If all the machines are in use, they join the queue. This is represented by the arrival rule in the queue state variable -- it is incremented by one if 'full' is true. Alternatively, if there is a free machine, the new customer starts using the first available one. To identify the first free machine, the machine submodel contains the 'unreached' variable, which is true for each machine if there is a free machine before that one. i.e., if the previous machine is either unreached or free. Only one machine will be reached and free, and this is the one a new customer starts using.
The time a customer takes on a machine is also a statistical function, in this case a sample from a Gaussian distribution. The 'finish using' event occurs a certain time after 'start using', and one of two things can happen. If there are queueing customers, i.e., 'queue' is nonzero, a customer leaves the queue ('de-queue' rule for queue state) and another start-using event immediately occurs. Otherwise the machine becomes free.
Running the model shows that with the given frequency and use times, there is very little queueing, but once a queue is started it can get quite long and take a long time to clear. It is left as an exercise for the modeller to add extra components to compute statistics for the percentage of customers who have to queue and the average waiting time for those who do.
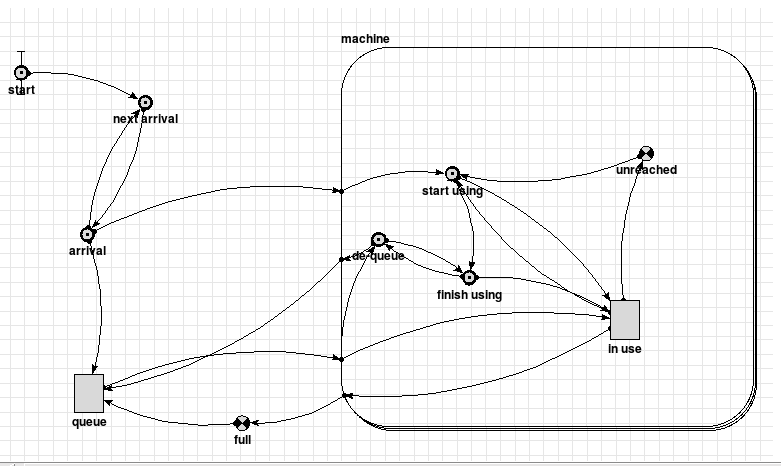
Model Desktop1 :
Event arrival : Customer arrives
arrival = "true" (boolean)
Comments:
This happens after a wait from the beginning of the simulation or from the last customer arrival
Event next arrival : Wait for customer arrival
next arrival = after(exprnd(4),"true") (boolean)
Comments:
Customers arrive ar random intervals, so time between arrivals is given by the exponential distribution. Wait starts either at start of simulation or on arrival of previous customer.
Event start : Start of simulation
start = time() (boolean)
Maximum = 0
Comments:
Provides an event at time 0, the start of the simulation.
State queue : Number of customers waiting
queue = [[arrival,prev(0)+(if full then 1 else 0)],[reset...,0],[machine/de-queue,prev(0)-1]] (int)
Where:
full = Value(s) of full
Comments:
This starts at zero, increases by 1 if a customer arrives when all machines are full, and decreases by one when a customer leaves the queue
Variable full : All machines are in use
full = all([in_use]) (boolean)
Where:
[in_use] = Value(s) of machine/in use
Submodel machine :
Submodel "machine" is a fixed_membership multi-instance submodel with dimensions [3].
Event de-queue : Customer moves from queue to machine
de-queue = queue>0 (boolean)
Where:
queue = Value(s) of ../queue
Comments:
Happens if someone finishes using a machine while people are waiting
Event finish using : Customer completes transaction
finish using = after(gaussian_var(10,1),"true") (boolean)
Comments:
A period of time sampled from a normal distribution has elapsed since the customer started using the machine. Customer either started using machine which was idle, or came out of the queue.
Event start using : Machine comes into use
start using = not unreached and not in_use (boolean)
Where:
in_use = Value(s) of in use
unreached = Value(s) of unreached
Comments:
Happens when this is the first free machine and a customer arrives and starts using it immediately
State in use : Machine is busy.
in use = [[finish using,queue>0],[start using,"true"],[reset...,"false"]] (boolean)
Where:
queue = Value(s) of ../queue
Comments:
Machine becomes busy when a customer arrives and starts using it, and remains busy until a customer finishes using it while the queue is empty.
Variable unreached : New customers do not reach this machine
unreached = in_preceding(prev(0) or not in_use) (boolean)
Where:
in_use = Value(s) of in use
Comments:
There is an unused machine earlier in the group than this one. Either the last machine is itself unreached or it is not in use.
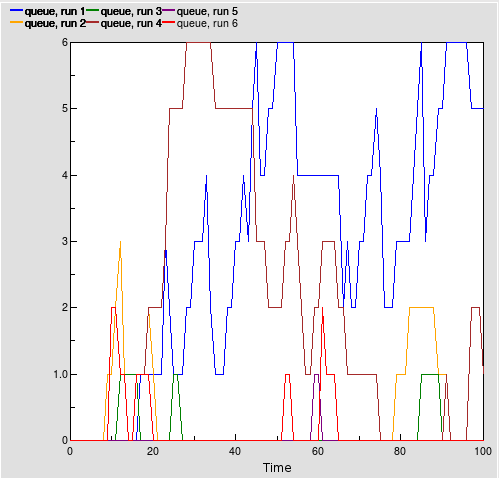
This graph shows results for six consecutive runs superposed. Only the blue and brown runs show significant queueing.
