Main menu
You are here
Skeleton cohort model
This example shows how to implement a basic cohort model in Simile.
A cohort model is one way of modelling a population. The individuals are grouped into cohorts, typically on the basis that they were born at the same time. Each cohort has as a minimum a variable representing the number of individuals in that cohort, along with possibly other cohort-specific attributes, such as the average size of the individuals in the cohort.
Thus, the objects in the model are not the individuals themselves, but the cohorts. We therefore use the Simile 'population submodel' to represent the cohorts.
A cohort comes into existence at some point in time - typically, one new cohort is created each time unit. A cohort ceases to exist when the value for the number of individuals in it becomes zero.
In the simplest case, there is no interaction between cohorts. However, there often is some form of interaction - for example, a cohort model of the trees in a forest might need to include the fact that the larger trees reduce the growth of smaller trees, by shading. This requires that we represent an association between cohorts, so that we can work out the total impact (in the case of tress, from shading) of all the trees in the cohorts which are bigger than a particular cohort.
The skeleton model shown here captures these concepts, and consists of two submodels. This is a discrete-time model, with a time step equal to 1 time unit (say, year).
Diagram
Here is the model diagram for the simple cohort model:
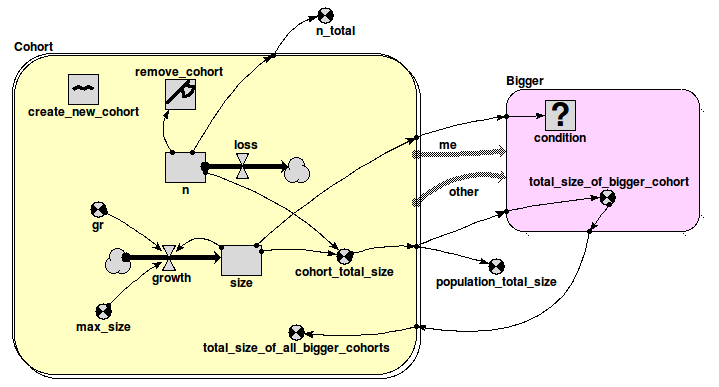
The submodel 'Cohort' is a Simile 'population submodel'. The 'create_new_cohort' symbol is a Simile 'immigration' symbol, and has a value of 1 - this means that 1 new cohort is created each time step. The number of individuals in the cohort is represented by the compartment 'n', and is set initially to zero. The outflow reduces the number by 5 each time step. The size of the average individual in the cohort is represented by the compartment 'size', and increases at an initial rate 'gr' up to an asymptote given by 'size_max'. At any point in time, the 'cohort_total_size' is the size of each individual multiplied by the number of individuals.
The submodel 'Bigger' represents an association (relationship) which exists between a pair of cohorts, when one of them is bigger than the other (in terms of the 'size' compartment). This submodel is used to transfer values for the 'cohort_total_size' from the bigger to the smaller cohort.
For each cohort, all the total-size values for the cohorts which are bigger than it is are summed up in the variable 'total_size_of_all_bigger_cohorts'. To make the functioning of the model clearer, this value is *not* used in this skeleton model to reduce the growth rate of the cohort. However, it is easy to do this - just take an influence to 'growth' and put in some inverse relationship.
Variable: n_total = sum({n})
Where: {n} = Cohort/n
Variable: population_total_size = sum({cohort_total_size})
Where: {cohort_total_size} = Cohort/cohort_total_size
--------------------------------------------------------------
Submodel Bigger
Submodel "Bigger" is an association submodel between "Cohort" and itself with roles "other" and "me".
Condition: condition = other_size>me_size
Where:
me_size = Value(s) of ../Cohort/size from submodel "Cohort" in role "me"
other_size = Value(s) of ../Cohort/size from submodel "Cohort" in role "other"
Variable: total_size_of_bigger_cohort = other_cohort_total_size
Where:
me_cohort_total_size = Value(s) of ../Cohort/cohort_total_size from submodel "Cohort" in role "me"
other_cohort_total_size = Value(s) of ../Cohort/cohort_total_size from submodel "Cohort" in role "other"
-------------------------------------------------------------------------
Submodel Cohort
Submodel "Cohort" is a population submodel.
Compartment: n
Initial value = 100
Rate of change = - loss
Compartment: size
Initial value = 0
Rate of change = + growth
Flow: growth = gr*(1-size/max_size)
Flow: loss = 5
Immigration: create_new_cohort = 1
Loss: remove_cohort = n<=0
Variable: cohort_total_size = n*size
Variable: gr = 1.5
Variable: max_size = 10
Variable: total_size_of_all_bigger_cohorts = sum({cohort_total_size_of_bigger_me})
Where:
{cohort_total_size_of_bigger_me} = ../Bigger/total_size_of_bigger_cohort for submodel "Cohort" in role "me"
The results shown here illustrate the basic functioning of this model.
The following figure shows a set of panels, each one showing the values for a specified variable at time 10. These were made using Simile's 'snapshot' tool, and enable us to trace the values as they are processed in the model.
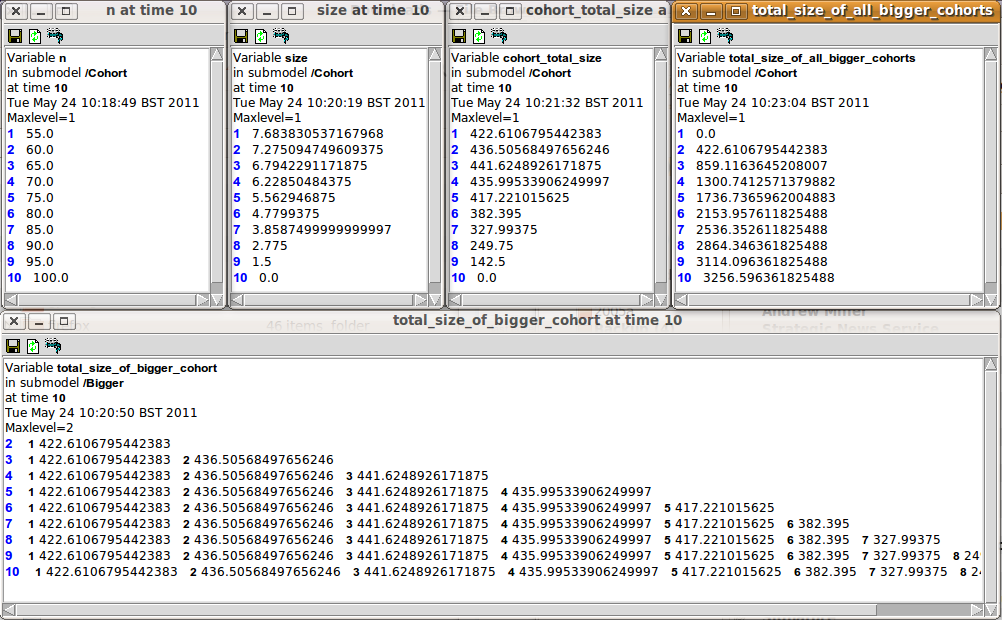
The first 3 panels on the top row show, for each of the 10 cohorts created up to this time, the number of tress (n) and the size of the average tree (size) in the cohort, along with the total size (n x size). You can see that the number of tress declines in a cohort declines by 5 each time step, and that the average tree in a cohort grows at a reducing rate as the cohort gets older.
The bottom window shows the total_size values for the individual cohorts that are bigger than the specified cohort. Thus, cohort 2 only has one value (since there is only one bigger than it is), while cohort 3 has 2 values, and so on.
The top-right window shows 'total_size_of_all_bigger_cohorts' - the sum (along a row) for al the total_size values of bigger cohorts for a particular cohort. This is the key value which enables the impact of bigger cohorts on the growth of a cohort to be modelled.
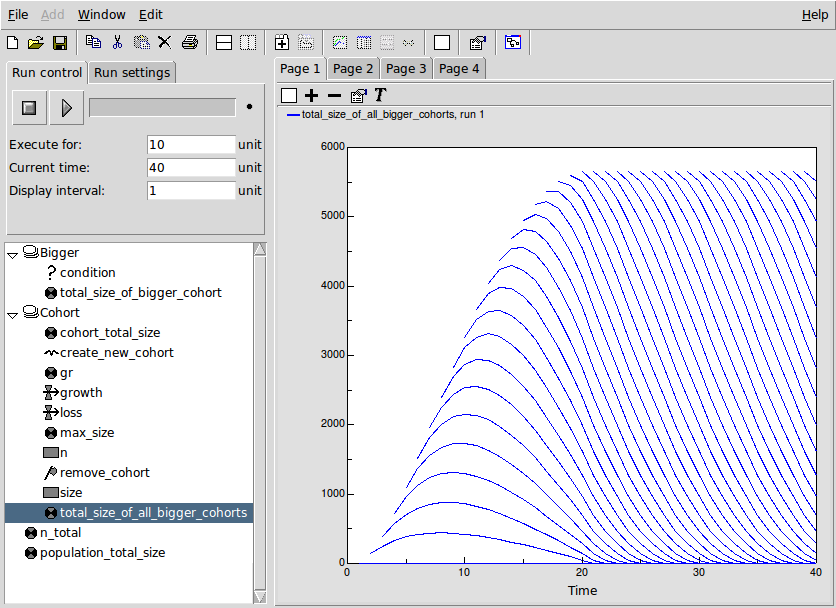
The graph below shows how the 'total_size_of_all_bigger_cohorts' changes over time, for each cohort. The lowest curve is for the second cohort (since the first cohort has nothing bigger than it. Each successive cohort starts off at a higher value (since the total size of cohorts above it is increasing), until we get to the point where each newly-created cohort starts off with the same total_size above it, which decreases as that cohort in turn increases in size.
| Attachment | Size |
|---|---|
| 190.79 KB | |
| 2.82 KB |
