Conditional submodels

A conditional submodel specifies the conditions under which a submodel, or an instance of a fixed-membership multiple-instance submodel, exists. By "exist" we mean that Simile evaluates the expressions in the submodel. It does this by evaluating a Boolean expression in a 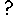condition symbol placed inside the submodel.

If the submodel has influence arrows going from inside to variables outside itself, then:

• if the submodel exists, the values emerging from the submodel are those calculated from the variables in the normal way;
• if the submodel (or instance of it) does not exist, then a value is not exported for each variable: there is no value, since the variable just doesn't exist.

This means that we cannot be sure how many values are going to be exported from a single variable inside the conditional submodel. For a simple submodel, there could be zero or one values. For a fixed-membership multiple-instance submodel, there could be 0…n values, where n is the number of instances for the submodel.

Therefore values are always exported as a list from a conditional model, since a list (as opposed to an array) is the data structure used when the number of values in the data structure can vary dynamically over time. A list must be processed as soon as it is received: it cannot be passed around as a persistent data structure. Typically, you will simply use the sum function to add the values in the list together.

In: Contents >> Working with submodels