Main menu
You are here
Embryo morphogenesis
This model implements ideas developed by John Gurdon, Cambridge University, on the role of activin in morphogenesis. The following gives a biological statement about the system on the left, and the corresponding Simile realisation on the right.
Biology |
Simile model |
|
The model represents a 2D plane of 'cells' in the growing embryo. As discussed below, it is very easy to change the model to represent a 1D linear arrangement of cells, or a 3D volume of cells. Each 'cell' actualy represents a unit of space, containing both an actual biological cell, plus the intercellular space around the cell. |
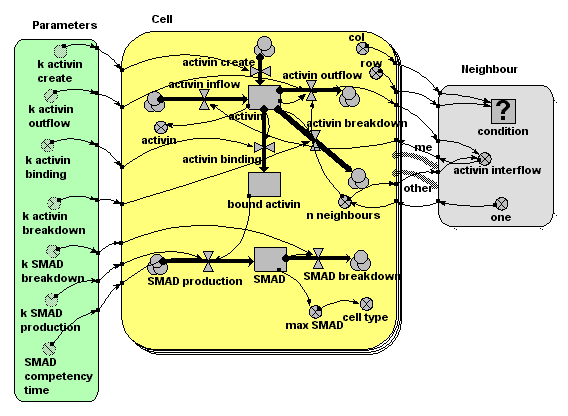
In the Simile model, we use a submodel, 'Cell', to represent a unit cell. There are a fixed number of these, as denoted by the multiple ('stacked card') boundary in the model diagram. In the model run here, there are 400 ( = 20x20) instances of the Cell submodel, but the model can run happily with much larger numbers. Each cell has row and column attributes (i.e. it knows where it is in the grid of cells): these are worked out using a built-in function (index(1)), which returns the instance number of each instance of a submodel. Cells know who their immediate neighbours are. This is represented by the 'association submodel' 'neighbour'. This has two 'role arrows', both pointing to it from the Cell submodel, indicating that cells are neighbours with other cells. The association depends on the coordinates of each of the two cells: this is represented by the influence arrows coming from the x,y variables of Cell to the condition |
|
A source site produces activin at a constant rate, for a limited period of time (say, minutes 10 to 20). This diffuses across the plane of cells, with the amount moving from one cell to the next being proportional to the amount in the donor cell. This means that the flow across a boundary is actually calculated twice, with each cell being the donor cell in turn. This produces exactly the same results as calculating the flow once, using a simple 'flow-across-a-gradient' expression: the method used here is easier to implement, at some (acceptable) computational cost. |
The amount of activin in the intercellular space around each cell is represented by a compartment (state variable) 'activin'. The amount at any one location changes over time through the effect of four processes, each represented by a flow. One is concerned with producing new activin. This is conditional on time and cell number, operating only in cell 5 (location 1,5) between minutes 10 and 20. This is the point source production of activin. One flow is concerned with breaking down activin, at a rate proportional to amount. Two flow are concerned with moving activing across the grid. One represents the total amount of activin diffusing out of the cell’s extra-cellular space into that of neighbouring cells. The other represents the total inflow from the extra-cellular space of the eight neighbouring cells into that of each cell. The outflow is processed through the neighbour association submodel, enabling each cell to calculate its inflow as the sum of one-eightth of the outflow from its eight neighbours. |
|
Some of the activin binds to receptor sites on the surface of each cell. This occurs at a rate which depends on the amount of activin in the intercellular space around the cell. Once bound, the activin remains bound to the receptor site. |
We represent the amount of bound activin using another compartment. It has an inflow representing the binding process, and no outflow, since no bound activin becomes unbound. The rate of binding depends on the amount of activin around that cell. |
|
Each cell produces the internal chemical messenger SMAD at a rate proportional to the number of activin molecules bound to receptors. (Research has shown that it is indeed the absolute number of bound receptor sites that is critical, not the proportion of sites). SMAD 'competence' (i.e. the ability of the cell to produce SMAD when activin receptor sites are occupied) stops suddenly at a certain point in time. SMAD breaks down at a concentration-dependent rate. |
Each cell has a compartment (state variable) representing the amount of SMAD. The inflow represents SMAD production, at a rate dependent on the number of activin-occupied receptor sites. Production also depends on simulation time (not shown on the diagram but represented in the flow equation using the built-in function “time( )”). The SMAD breakdown outflow occurs at a rate proportional to the amount of SMAD. |
|
Research has shown that which genes are switched on depends on the maximum amount of SMAD experienced by the cell. |
The variable 'max SMAD' is used to remember the maximum value of the SMAD compartment. It is actually a state variable (i.e. it has memory of its previous state, using the function “prev(1)”, which returns the previous value of a variable. |
The animation below shows the activin concentration on the left; the SMAD concentrations in the middle, and the resulting cell commitment to cell type on the right.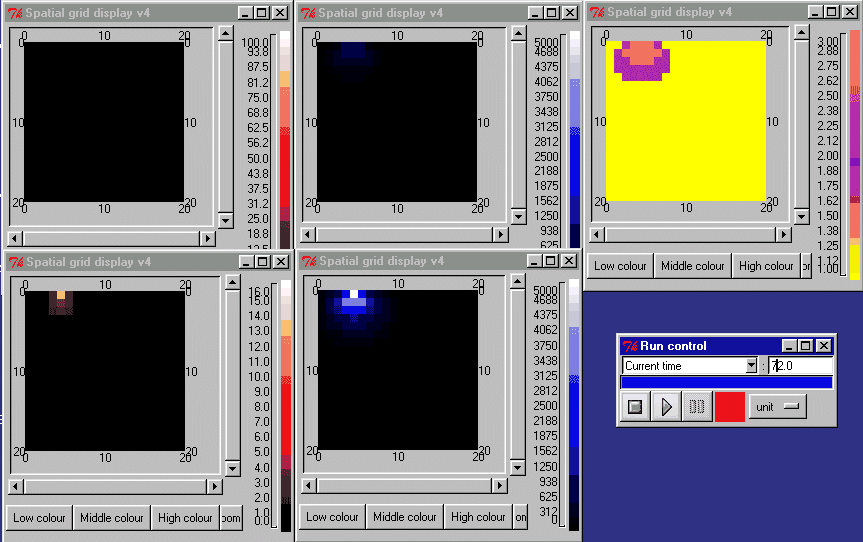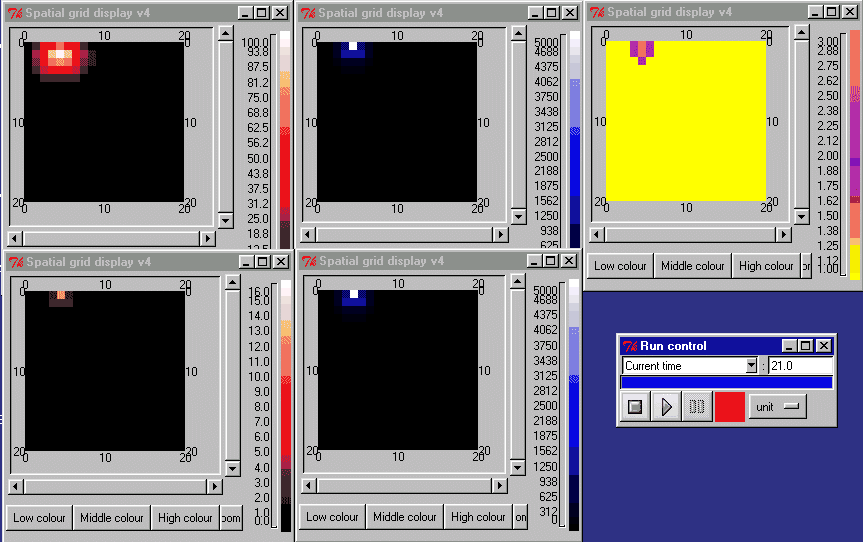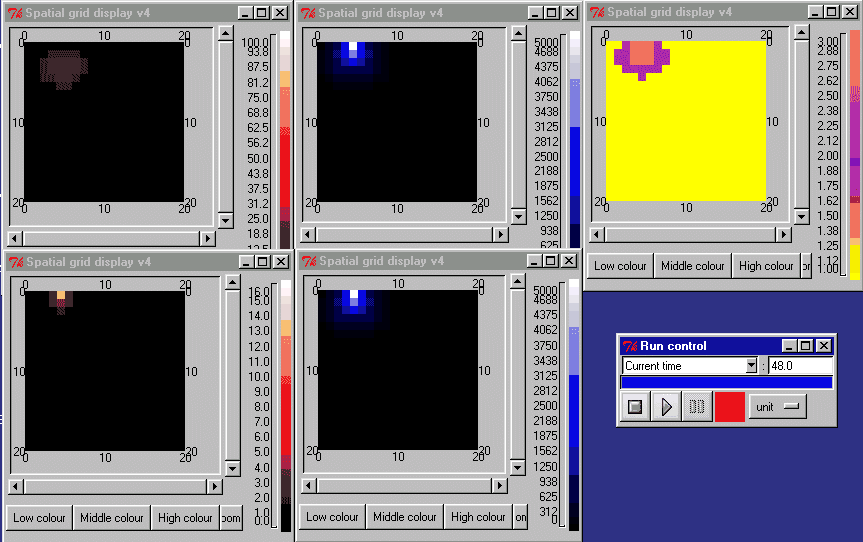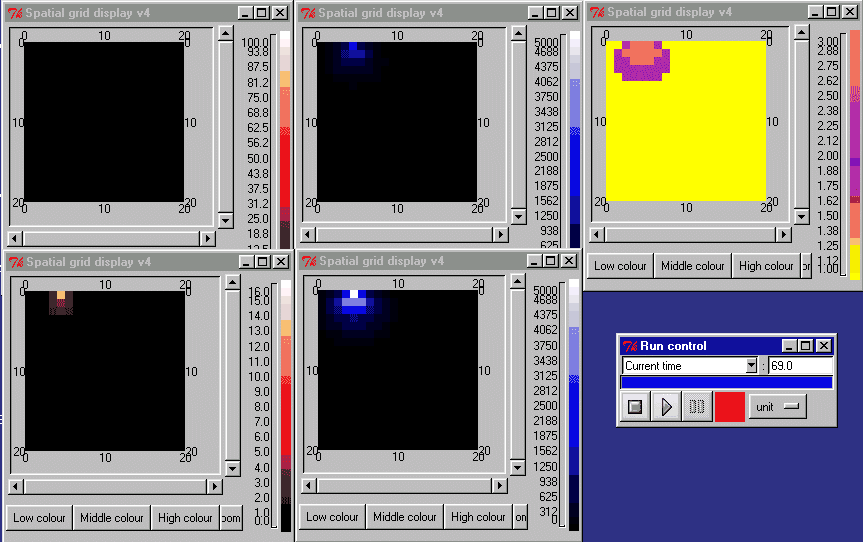
| Attachment | Size |
|---|---|
| 112.98 KB |
