Model Gallery

You can use this page to get a quick overview of the wide range of models that can be constructed in Simile. Each entry gives some text on the model, a model diagram (usually an outline view for all but the simplest of models), and a sample screen display from the running model. Models are arranged roughly in order of increasing complexity and increasing sophistication of the Simile techniques used.

Classic (Lotka-Volterra) population dynamics

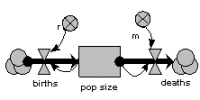
Exponential population growth

The population is represented by a single state variable (compartment), whose dynamics depends on two flows: a reproduction inflow and a mortality outflow. Both occur at a rate proportional to population size, where r and m are the coefficients of proportionality.

The graph shows the expected exponential increase in population size.

Logistic (sigmoid, density-dependent) population growth

The previous model is modified by making r, the reproductive rate per individual, depend on population size, decreasing as population increases.

This causes the population to grow roughly exponentially to begin with, but then rise more slowly towards a “carrying capacity”.

Two-species competition

Each population grows logistically in the absence of competition, with its growth rate reduced as its population gets bigger. When a competitor is present, then the growth of each population is further reduced by the other. The outcome depends on the relative strength of within- and between-species factors.

The graph shows that both species initially grow at similar rates, but then species 1 escapes and suppresses species 2.

Predator – prey

The prey (N1) grows exponentially in the absence of predation. It is predated at a rate proportional to the number of predators. The growth rate of the predator propulation is proportional to prey consumption, and predator mortality is proportional to its population.

This model shows the classic (but rather mythical) predator-prey cycle.