Main menu
You are here
Area covered in "flowers" compared with logistic growth model
This models the spatial spread of vegetation over an area. Here, the vegetation is taken to be �flowers�. This is not a spatial model, in the usual sense where space is divided up into discrete units. Rather, the area covered by the flowers is represented by a single state variable, with an inflow representing increase in area (spread), and an outflow representing decrease in area (death of flowers).
This is actually two models in one: a dynamic model of the spatial spread of the flowers, and the analytical form of the logistic growth equation, to enable the two to be compared.
Note that this illustrates a useful tip for comparing two models: put them into the same Simile model, so that they will be running in parallel. You can then produce a single graph or table comparing the behaviour of matching variables from the two models. Enclosing each of the two models in its own submodel envelope would make the separateness of the two models visually clearer.
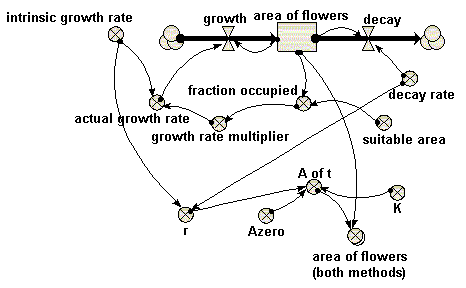
Compartments:
area of flowers
Initial value = 10
Rate of change = + growth + decay
Comments: hectares (OK, Ford says acres, but we are in the 21st century now).
Flows:
decay = area_of_flowers*decay_rate
growth = area_of_flowers*actual_growth_rate
Variables:
A of t = Azero*exp(r*time(1))/(1+Azero*(exp(r*time(1))-1)/K)
actual growth rate = intrinsic_growth_rate*growth_rate_multiplier
Comments: dimensionless
area of flowers (both methods) = [area_of_flowers,A_of_t]
fraction occupied = area_of_flowers/suitable_area
growth rate multiplier = graph(fraction_occupied)
intrinsic growth rate = 1
Comments: I.e. 100% per year
Parameters:
Azero = 10
Comments: Initial area of flowers (hectare)
decay rate = 0.2
Comments: Proportion decaying (per year)
K = 800
Comments: "Maximum value that the flowered area would reach over time"
r = intrinsic_growth_rate-decay_rate
suitable area = 1000
Comments: hectares (see 'area of flowers'...)

Ford, A (1999) Modeling the Environment.
| Attachment | Size |
|---|---|
| 41.79 KB |
