One-compartment mixing process

Model : Muller1-1a
Simile version : 4.0
Date added : 2004-10-27
Keywords : Mixing, solution ; Basic System Dynamics ;

Description

This model illustrates the use of System Dynamics to model a simple mixing process. It is model Mod1-1a of Muller (2000) implemented here in Simile.

The system comprises a flask with an inlet and an outlet containing a volume of salt solution of one concentration. Solution is pumped in and out at the same rate. The in-flow of salt solution is of another concentration. Assuming the contents of the flask is well mixed, what is the concentration of the solution in the outlet over time.

Simile integrates using numerical methods, either Euler or 4th-order Runge-Kutta. The second is more accurate for truly continuous variables but fails if discontinuities (step changes) are present. Because of this the Euler method is used by default in Simile as many models include step changes. However, the system described here is continuous and the 4th-order Runge-Kutta performs better. This problem can be solved analytically and the equation for Wsalt_analytical does so allowing the numerical methods used by Simile to be evaluated. Have a play changing the integration method and time step. The results section shows a couple of runs of the model with different integration method setting.

Files

Model file Click on the icon to download the model file. (You will need Simile to examine and run the model. A free evaluation version is available from the products page.) Some browsers may attempt to display the model file, rather than open it in Simile; in this case, use the browser back button to return to this page, and use the context menu (invoked by right-clicking on the link) to save the target file to disk.

Mod1-1aP.sml

Diagram

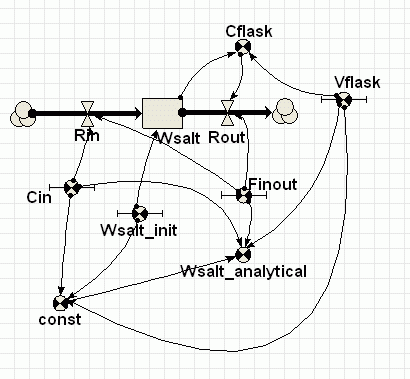
Equations

Compartment   Wsalt : g
	Initial value = Wsalt_init
	Rate of change =  + Rin - Rout
 
Flow   Rin
	Rin = Cin*Fin 
	Where:
		Fin=Finout 
 
Flow   Rout
	Rout = Cflask*Finout 
 
Variable   Cflask
	Cflask = Wsalt/Vflask 
	Comments:
		g/l 
 
Variable   Wsalt_analytical
	Wsalt_analytical = -(Vflask*(exp(-(Finout*time(0)+const)/Vflask)-Cin)) 
 
Variable   const
	const = -(log(Cin-Wsalt_init/Vflask)*Vflask) 

Results

Integration method: Euler Time step : 0.1

Integration method: 4th-order Runge-Kutta Time step : 0.5
N.B. The traces for the analytical and the numeric, 4th-order Runge-Kutta, intergration overlap.

References

Muller, C. 2000 Modelling soil-biosphere interactions. CABI Publishing Oxford and New York pp 354

Copyright 2003-2024 Simulistics Ltd