Search

Simulistics

Model catalogue

Listed by keyword

Listed by ID

Listed by title

Listed by date added

A hierarchy of hexagonal tilings

Model : hex_levels
Simile version : 4.0
Date added : 2004-11-19
Keywords : Association submodel ; Dashed influence arrow ; Dummy instance ; Exclusive Role ; Hexagonal grid ; One sided enumeration ;

Description

This model has been included to illustrate a number of techniques used to create complex structures in which model components can interact. It allows an area to be represented as a series of hexagonal tilings, with increasing levels of detail. Each hexagon in one level corresponds to a group of 7 hexagons in the next level down. The arrangement is based on that used in the HOOFS model (S. P. Oom et al, 2004)

It would be straightforward to implement this layout with a series of nested submodels, each representing one layer of the tiling. In this case, each submodel would have dimensions of 7, corresponding to the 7 hexagons at a lower level that fill a single hexagon at a higher level. However, since several variables are needed in each level to keep the hexagon's position and vertex coordinates, it is more elegant to have all the hexagons at all levels represented by instances of a single submodel, with an association to represent the parent-child relation between them.

This example has hexagons at six levels, the top level consisting of just one hexagon, the bottom of 7^5 or 16807 hexagons. The hexagon submodel has 19608 members, that being the total number of hexagons at all levels. The parent-child association connects hexagons with other hexagons. If it were to be enumerated by checking every pair for a parent-child relationship it would have to do nearly 400 million checks, which would be too slow. Therefore a technique called one-sided enumeration is used.

To do this, each hexagon calculates the id of its parent. This is straightforward as the children of all parents are in the same order as the parents themselves. The role arrow from the parent instance (higher) is then marked 'allow base instance lookup', and the existence condition in the association submodel starts 'index(1) is...' which allows the association to be set up by directly looking up the parent instance from each child instance.

Now child instances must get some information from their parents. Firstly they must get their level, which is one greater than that of their parents. This is used to access information from the corresponding instance of the submodel 'level info', for, e.g., the offsets of their centres from the parent's. So the parent's level is fed into the association model and taken out by the child, which adds 1 to get its own level.

Because the association is exclusive for the child, there is only one parent level value for each child. This makes the model simpler, but creates a problem when setting the level of the top level hexagon. The problem is that the base model values are set for each association model, so it will only get a value at all if it has the child role in some association. This is solved by adding a dummy instance of the association, connecting the top level hexagom with itself. In this case, the equation for the 'my parent' variable has a clause that sets it to 1 for instance 1, when it would otherwise be 0. The 'dummy' variable in the association model is true for the instance resulting from this clause (linking hexagon 1 with itself) and this variable is used to make sure that in this instance the information being passed to the child hexagon is that needed by the top-level hexagon, rather than trying (and failing) to get it from the parent hexagon.

Also note the dashed influence arrows going from the hexagon submodel to the parent/child association. These are created by selecting 'use in same time step' in the influence properties. The purpose of this feature is to indicate how the model should be built in the case of an apparent circular set of influences. The circularity occurs because each hexagon instance's level (and other properties) is set from the association, while the level values for the associations are set from the hexagons. Making a dashed influence to the association means that the value in the association can be set without waiting for all the values in the hexagon submodels to be calculated. This makes it work properly because also,

• Since the child hexagon is an exclusive role, values in the child that come from the association are set at the same point in the program as values in the association itself (see discussion on dummy instances above)
• The association model instances are in the order of the indices of the base models.

Thus, the first association gets the right value because of the special clause for the dummy instance, and the first hexagon (which is the child in the dummy association) gets level 1 from the dummy. The second to eighth hexagons get level 2 because when they are evaluated the right level has already been set for their parent, hexagon 1, and the association picks it up without waiting for the child values to be calculated, and so on, till they all have the right level.

Finally, there is a conditional submodel 'for display' which exists within the hexagon submodel and exists only for those of a particular level. This is where the hexagon vertices are calculated, and the condition ensures only the vertices of a particular level are done, simply so the polygon display tool can be used to show the polygons at one level. This is currently the bottom level, level 6, but the model can be changed to display hexagons at higher levels.

Files

Model file Click on the icon to download the model file. (You will need Simile to examine and run the model. A free evaluation version is available from the products page.) Some browsers may attempt to display the model file, rather than open it in Simile; in this case, use the browser back button to return to this page, and use the context menu (invoked by right-clicking on the link) to save the target file to disk.
oom2.sml
oom2.shf	Helper setup file

Diagram

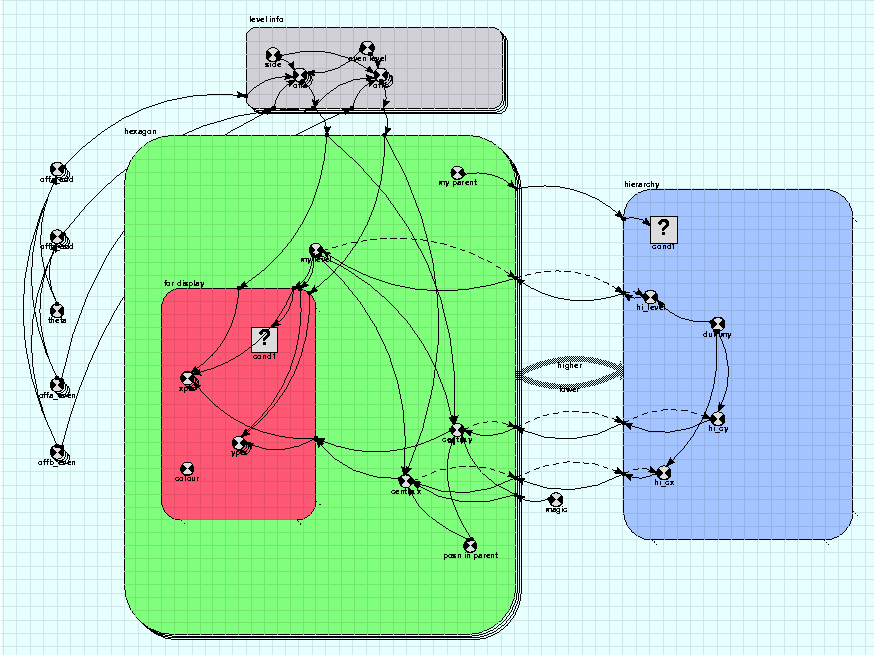
Equations

Equations in top level
 
Variable   magic
	magic = sqrt(3) 
 
Variable   offa_even
	offa_even = [ 0.5, -0.5,-1, -0.5, 0.5,1] 
 
Variable   offa_odd
	offa_odd = cos(theta)*[offa_even]-sin(theta)*[offb_even] 
 
Variable   offb_even
	offb_even = [ 0.866, 0.866,0, -0.866, -0.866,0] 
 
Variable   offb_odd
	offb_odd = sin(theta)*[offa_even]+cos(theta)*[offb_even] 
 
Variable   theta
	theta = atan(3*sqrt(3)) 

Equations in hexagon
 
Variable   centre x
	centre x = if posn_in_parent==0 then hi_cx_lower else hi_cx_lower+magic*element(element([[offb]],my_level),int(posn_in_parent)) 
	Where:
		my_level=my level
		posn_in_parent=posn in parent
		[[offb]]= ../level info/offb
		{hi_cx_higher}= ../hierarchy/hi_cx (to hexagon in higher)
		hi_cx_lower= ../hierarchy/hi_cx (to hexagon in lower)
		magic= ../magic 
 
Variable   centre y
	centre y = if posn_in_parent==0 then hi_cy_lower else hi_cy_lower-magic*element(element([[offa]],my_level),int(posn_in_parent)) 
	Where:
		my_level=my level
		posn_in_parent=posn in parent
		[[offa]]= ../level info/offa
		{hi_cy_higher}= ../hierarchy/hi_cy (to hexagon in higher)
		hi_cy_lower= ../hierarchy/hi_cy (to hexagon in lower)
		magic= ../magic 
 
Variable   my level
	my level = hi_level_lower+1 
	Where:
		{hi_level_higher}= ../hierarchy/hi_level (to hexagon in higher)
		hi_level_lower= ../hierarchy/hi_level (to hexagon in lower) 
 
Variable   my parent
	my parent = if index(1)==1 then 1 else int((index(1)+5)/7) 
 
Variable   posn in parent
	posn in parent = if index(1)==1 then 0 else int(fmod(index(1)-2,7)) 

Equations in hierarchy
 
Condition   cond1
	cond1 = index(1) is my_parent_lower 
	Where:
		my_parent_lower= ../hexagon/my parent (from hexagon in lower)
		my_parent_higher= ../hexagon/my parent (from hexagon in higher) 
 
Variable   dummy
	dummy = index(2)==1 
 
Variable   hi_cx
	hi_cx = if dummy then 0 else centre_x_higher 
	Where:
		centre_x_lower= ../hexagon/centre x (from hexagon in lower)
		centre_x_higher= ../hexagon/centre x (from hexagon in higher) 
 
Variable   hi_cy
	hi_cy = if dummy then 0 else centre_y_higher 
	Where:
		centre_y_lower= ../hexagon/centre y (from hexagon in lower)
		centre_y_higher= ../hexagon/centre y (from hexagon in higher) 
 
Variable   hi_level
	hi_level = if dummy then 0 else my_level_higher 
	Where:
		my_level_lower= ../hexagon/my level (from hexagon in lower)
		my_level_higher= ../hexagon/my level (from hexagon in higher) 

Equations in level info
 
Variable   even level
	even level = fmod(index(1),2)== 1.0 
 
Variable   offa
	offa = side*(if even_level then [offa_even] else [offa_odd]) 
	Where:
		even_level=even level
		[offa_even]= ../offa_even
		[offa_odd]= ../offa_odd 
 
Variable   offb
	offb = side*(if even_level then [offb_even] else [offb_odd]) 
	Where:
		even_level=even level
		[offb_even]= ../offb_even
		[offb_odd]= ../offb_odd 
 
Variable   side
	side = 50/7^((index(1)-1)/2) 

Equations in  for display
 
Condition   cond1
	cond1 = my_level==6 
	Where:
		my_level= ../my level 
 
Variable   colour
	colour = index(1) 
 
Variable   xpts
	xpts = centre_x+element([[offa]],my_level) 

	Where:
		centre_x= ../centre x
		[[offa]]= ../../level info/offa
		my_level= ../my level 
 
Variable   ypts
	ypts = centre_y+element([[offb]],my_level) 
	Where:
		centre_y= ../centre y
		[[offb]]= ../../level info/offb
		my_level= ../my level 

Results

|Here is the diagram of the hexagons at the lowest level: |

References

S.P. Oom, J.A. Beecham, C.J. Legg and A.J. Hester (2004) Foraging in a complex environment: from foraging strategies to emergent spatial properties
Ecological Complexity, 1(4) pp297--321. Online version

Copyright 2003-2024 Simulistics Ltd