Predation rates in a multiple prey species/multiple predator species system

Model : nprey_npred
Simile version : 4.8
Date added : 2007-03-03
Keywords :

Description

This implements the feeding part of predator-prey model with multiple prey species and multiple predator species. Each predator species predates the multiple prey species as per the "multiprey disc equation" developed by Charnov (1974), and reported in "Serengeti" (Eds Sinclair and Norton-Griffiths) (1979), p.295. This has been extended to cater for multiple predator species.

The disc equaltion for the functional response of one predator species feeding on one prey species is:
E = a*N/(1+h*a*N)
where:

• E = number of prey consumed by one predator per unit of time;
• N = prey density (numbers);
• a = "rate of search" of predator;
• h = "handling time" of predator for one prey item.

With multiple prey, the equation (for one predator species) becomes:
Ei = ai*Ni/(1+sum(j=1...N of hj*aj*Nj)

This model implements this equation for multiple predator species.

Note that this model has the bare bones required just for handling the predation interaction. It is not a complete predator-prey model, since the normal population processes (reproduction for prey and reproduction and mortality for predator) are not included. The only such process that is included is the prey mortality rate through predation, since that is a core element of the analysis. On the predator side, the variable 'total_weight_eaten' would normally be used to influence the predators' reproduction and mortality rates.

All values are artificial, to make it easier to see what's happening. The model is not intended to be run. Rather, you can:

• Load the model and prepare it for running, then mouse over the various variables, and try to understand the model by checking out their values.
• Use th emodel as a basis for your own model of predator-prey dynamics, adding in the required reproduction an dmortality flows, and adapting the parameter values as appropriate.

Files

Model file Click on the icon to download the model file. (You will need Simile to examine and run the model. A free evaluation version is available from the products page.) Some browsers may attempt to display the model file, rather than open it in Simile; in this case, use the browser back button to return to this page, and use the context menu (invoked by right-clicking on the link) to save the target file to disk.

nprey_npred.sml

Model fragment for predation between multiple predator and multiple prey species

Diagram

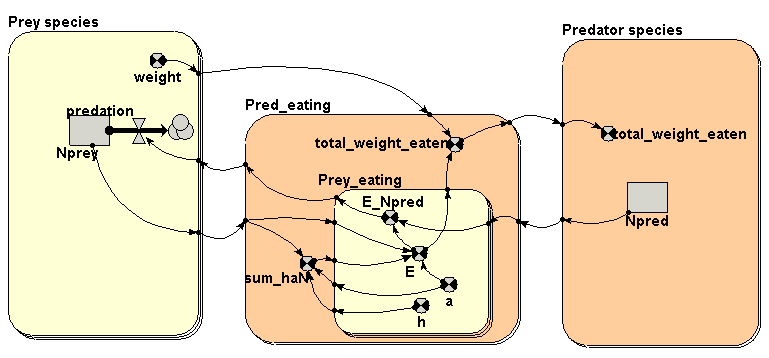
Equations

Submodel Prey species 
Submodel  Prey species is a fixed_membership submodel with dimensions [3].
Enumerated types: null
 
Compartment   Nprey
Initial value = element([100,200,300],index(1))
Rate of change =  - predation
 
Flow   predation
predation = element(sum([[E_Npred]]),index(1)) 
Where:
[[E_Npred]]=../Pred_eating/Prey_eating/E_Npred 
	
Variable   weight
weight = 	element([10,20,30],index(1)) 
	
Submodel Predator species 
Submodel  Predator species is a fixed_membership submodel with dimensions [2].
Enumerated types: null
 
Compartment   Npred
Initial value = element([1,2],index(1))
	
Variable   total_weight_eaten
total_weight_eaten = element([total_weight_eaten],index(1)) 
Where:
[total_weight_eaten]=../Pred_eating/total_weight_eaten 
	
Submodel Pred_eating 
Submodel  Pred_eating is a fixed_membership submodel with dimensions [2].
Enumerated types: null
 
Variable   sum_haN
sum_haN = sum([h]*[a]*[Nprey]) 
Where:
[Nprey]=../Prey species/Nprey
[h]=Prey_eating/h
[a]=Prey_eating/a 
	
Variable   total_weight_eaten
total_weight_eaten = sum([E]*[weight]) 
Where:
[E]=Prey_eating/E
[weight]=../Prey species/weight 
	
Submodel Pred_eating/Prey_eating 
Submodel  Pred_eating/Prey_eating is a fixed_membership submodel with dimensions [3].
Enumerated types: null
 
Variable   E
E = a*element([Nprey],index(1))/(1+sum_haN) 
Where:
[Nprey]=../../Prey species/Nprey
sum_haN=../sum_haN 
	
Variable   E_Npred
E_Npred = E*element([Npred],index(2)) 
Where:
[Npred]=../../Predator species/Npred 
	

Variable   a
a = element(element([[0.01,0.02,0.03],[0.02,0.04,0.06]],index(2)),index(1)) 
	
Variable   h
h = element(element([[0.1,0.2,0.3],[0.2,0.4,0.6]],index(2)),index(1)) 

Copyright 2003-2024 Simulistics Ltd